Differential Equations for Engineers
About This Course
This course is about differential equations and covers material that all engineers should know. Both basic theory and applications are taught. In the first five weeks we will learn about ordinary differential equations, and in the final week, partial differential equations.
The course is composed of 56 short lecture videos, with a few simple problems to solve following each lecture. And after each substantial topic, there is a short practice quiz. Solutions to the problems and practice quizzes can be found in instructor-provided lecture notes. There are a total of six weeks in the course, and at the end of each week there is an assessed quiz. Lecture notes can be downloaded from http://www.math.ust.hk/~machas/differential-equations-for-engineers.pdf
Course Syllabus
First-Order Differential Equations
-A differential equation is an equation for a function with one or more of its derivatives. We introduce differential equations and classify them. We then learn about the Euler method for numerically solving a first-order ordinary differential equation (ode). Then we learn analytical methods for solving separable and linear first-order odes. An explanation of the theory is followed by illustrative solutions of some simple odes. Finally, we learn about three real-world examples of first-order odes: compound interest, terminal velocity of a falling mass, and the resistor-capacitor electrical circuit.
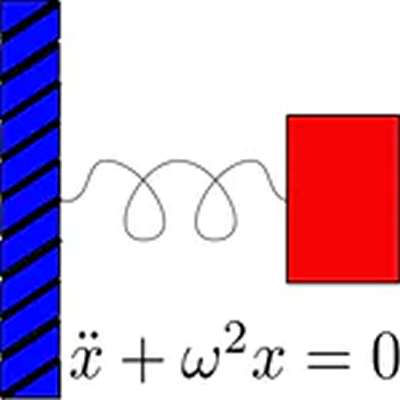
Homogeneous Linear Differential Equations
-We generalize the Euler numerical method to a second-order ode. We then develop two theoretical concepts used for linear equations: the principle of superposition, and the Wronskian. Armed with these concepts, we can find analytical solutions to a homogeneous second-order ode with constant coefficients. We make use of an exponential ansatz, and transform the constant-coefficient ode to a quadratic equation called the characteristic equation of the ode. The characteristic equation may have real or complex roots and we learn solution methods for the different cases.
Inhomogeneous Linear Differential Equations
-We now add an inhomogeneous term to the constant-coefficient ode. The inhomogeneous term may be an exponential, a sine or cosine, or a polynomial. We also study the phenomena of resonance, when the forcing frequency is equal to the natural frequency of the oscillator. Finally, we learn about three important applications: the RLC electrical circuit, a mass on a spring, and the pendulum.
The Laplace Transform and Series Solution Methods
-We present two new analytical solution methods for solving linear odes. The first is the Laplace transform method, which is used to solve the constant-coefficient ode with a discontinuous or impulsive inhomogeneous term. The Laplace transform is a good vehicle in general for introducing sophisticated integral transform techniques within an easily understandable context. We also discuss the series solution of a linear ode. Although we do not go deeply here, an introduction to this technique may be useful to students that encounter it again in more advanced courses.
Systems of Differential Equations
-We learn how to solve a coupled system of homogeneous first-order differential equations with constant coefficients. This system of odes can be written in matrix form, and we learn how to convert these equations into a standard matrix algebra eigenvalue problem. The two-dimensional solutions are visualized using phase portraits. We then learn about the important application of coupled harmonic oscillators and the calculation of normal modes. The normal modes are those motions for which the individual masses that make up the system oscillate with the same frequency.
Partial Differential Equations
-To learn how to solve a partial differential equation (pde), we first define a Fourier series. We then derive the one-dimensional diffusion equation, which is a pde for the diffusion of a dye in a pipe. We proceed to solve this pde using the method of separation of variables.
Course presenter

Jeffrey R. Chasnov
Professor
Bio
Jeffrey R. Chasnov is a Professor of Mathematics at the Hong Kong University of Science and Technology, where he has been teaching since 1993. He is an expatriate American from New York and California, and earned his BA from UC Berkeley and PhD from Columbia University, with post-doctoral fellowships at NASA, Stanford, and Grenoble, France, and a sabbatical semester at Harvey Mudd College. He is the author of numerous research articles in fluid turbulence and mathematical biology, and has authored online textbooks and videos for his courses on differential equations, matrix algebra, mathematical biology and scientific computation. Before and after work, he enjoys family life, swimming and tennis, and takes great pleasure in his family’s annual camping and skiing vacations.
FAQ
What is Coursera?
Coursera is an online education provider that offers online courses, popularly known as MOOCs or Massive Open Online Courses, from top universities around the world. Currently it has over 200 partners from 48 countries. These partners include Universities such as Stanford, Duke, Penn, Princeton, Michigan, Peking, and HEC Paris. Coursera has also started partnering with companies like IBM, Google, and PwC — these companies are also launching courses on Coursera.
Coursera is the most popular MOOC provider in the world based on the number of students (over 45 million learners) and has an active catalog of 3,800+ online courses.
As well as these individual courses and 16 online degrees, Coursera offers 400 groups of courses known as Specializations, MasterTracks, and Professional Certificates.
How do Coursera courses work?
Coursera is an online education provider that offers online courses, popularly known as MOOCs or Massive Open Online Courses, from top universities around the world. Currently, Coursera boasts an active catalog of more than 3800 online courses created by these partner institutions.
Coursera courses consist of pre-recorded video lectures that you can watch on a weekly schedule or when it’s convenient for you. They also have student discussion forums, homework/assignments, and online quizzes or exams.
Generally speaking, Coursera courses are free to audit (i.e. watch videos) but if you want to earn a course Certificate, you will need to pay. An investigation by Class Central discovered 1150+ Coursera courses that include assessments for free although other courses have the assessments behind a paywall.
Many of the Coursera courses are part of Coursera Specializations, a microcredential offered by Coursera. Specializations consist of a sequence of courses and for some Specializations the last course is a Capstone project. If learners earn a certificate for each course in a Specialization, they will receive a Specialization certificate. Specializations are usually geared towards in-demand skills in business and technology. You can take single courses or the whole specialization.
Other courses are grouped into MasterTracks and Professional Certificates. Coursera has launched over 400 microcredentials.
How does a Coursera Subscription work?
Some courses, particularly those in Coursera Specializations, are available on a subscription basis. When you sign up, the first 7 days are free, then you are charged monthly. Check the course or Specialization page to find the cost in US dollars or your local currency. You may also need to check the exchange rate to calculate the cost. The faster you learn, the less you will pay to complete the course or Specialization, in one-month increments.
If you want to complete one or some courses in a Specialization but not the whole Specialization, you need to cancel your subscription after receiving your certificate.
When signing up for Specializations, you cannot select the audit for free option, only a 7-day free trial. To access the materials for free, you need to sign up from the individual course pages. Click on the Learn more link beside the words at the bottom of each course description, available on some Specialization pages. (You can choose to take this course only.)
Coursera Plus is a single payment that gives access to around 3000 courses and Specializations for 12 months.